On this page I present a few modi of my field simulation program which for various reasons I did not put
on that page.
They all are based on the same principle, which I call wave equation with fiber potential
.
To explain it, I will go further afield mathematically.
The field $\psi$ is a time-dependent, vector-valued function (could be generalized to a section in a vector bundle) on a manifold (here, I consider only the flat 2-torus). The time evolution of the $n$ vector components is determined by the equations $$\frac{\text d^2 \psi_i}{\text d t^2} = \Laplace \psi_i - \frac{\text d V(\psi)}{\text d \psi_i},\quad 1\leq i\leq n.$$ This is the wave equation together with an extra term that models the influence of a potential energy $V$. The potential energy depends only on the value of $\psi$, not directly on the point on the manifold, so it is a function on an $n$ dimensional space.
If one repeatedly removes (kinetic) energy from the field $\psi$ (which you can do using the Clear button), it will try to attain a state with as low as possible potential energy. Hence the shape of the set of minima of $V$ is important for understanding the phenomena that can occur.
In one of the simplest cases with $n=2$, the minimum has the form of a circle, also known as S¹. The graph of the associated potential may then look like this:
It is called a sombrero potential
and is described by the formula
$$ V(\psi) = \left(\psi_1^2+\psi_2^2-1\right)^2.$$
In the graphical rendering, the value of $\psi$, being a 2D vector, is encoded using color.
The length of the vector determines the brightness and the direction of the vector determines the hue angle.
In the following image, the coloring is shown together with the potential:
Here is an example video for the dynamics of the wave equation with this fiber potential:
At the beginning, everything is dark as $\psi$ is initialized with relatively small values.
However, this state is not stable, and $\psi$ falls
into the minimum of the potential;
but because the minimum is not unique, into a part of the minimum that differs from place to place.
Hence you see lighter regions forming which have different color.
The wave equation sees to it that everything is smooth.
But there are also black points. At those points, $\psi$ must become small for topological reasons: If you go along a loop
around such a point and map this motion using $\psi$, you will go around once in the circle shaped potential minimum.
When contracting the loop into a point in the domain of $\psi$, the image of the loop also contracts into a point.
To do this, it must necessarily leave the potential minimum. This happens, to keep the energy low, in a small region only; that region then appears as a black dot.
There are two sorts of stable black points: Those that, when orbited clockwise, yield the colors in the order red-green-blue, and those that yield
red-blue-green. These two kinds of topological defects with opposite charge
attract each other and annihilate so that only waves remain.
Like particles and antiparticles do.
But there are also one dimensional defects, called domain walls. They arise because $\psi$ has fallen into a minimum with $\psi_3=\pi$ on one side of the domain wall, and into a minimum with $\psi_3=-\pi$ on the other side. For energy related reasons, the point defects like to sit on the domain walls, but they can also detach again.
Mainly when a domain wall contracts to a point and disappears, a third kind of phenomenon appears: Blinking, slowly crawling wave packets, called breather solitons. I assume that they come about due to the relatedness to the Sine-Gordon equation. The breather solitons are able to cross a domain wall if they hit it at a close to right angle.
Here is the example video:
Sometimes you can see a big black dot. It is formed due to a local change of the potential caused by the interaction of the mouse pointer with the simulation. I use it to drag around the domain walls and to generate breather solitons. It can also be used to drag point defects.
This mode uses the same formula as the previous, but a different color scheme that better brings out the point defects. In the example video you can see the rare phenomenon that two point defects (the last two remaining) do not immediately annihilate. Instead, a pair of points originates in the collision, which moves apart for a short time before it reunites and is finally converted into waves.
Here is the video:
In this mode, the potential is three dimensional. The minima are situated on three pairwise orthogonal great circles of the unit sphere. Thus, like an inflated octahedron, eight rectangular equilateral spherical triangles arise. These correspond to eight different kinds of topological defects and the corresponding anti-defects. To enhance the visibility of the defects, the visualization reduces the brightness of points that have a high value of the potential. The defects look triangular.
There are also round defects. They correspond to a loop around one of the great circles and develop from the unification of four defects that belong to the four spherical triangles of one hemisphere. The round defects often immediately decay into four triangular ones, which are then the anti-defects belonging to the four triangles of the other hemisphere. These can then reunite into a round defect, so that there is an oscillation between the two four particle states. You can discern this by the fact that the color in between the four triangle defects is replaced by its complementary color after the unification and subsequent decay.
In the example video you can also observe another interesting interaction: six triangle defects react to form two anti-trinagle defects. To wit, if a loop around the six defects is mapped using $\psi$, one gets a loop that goes around six spherical triangles. But that is the same as if one goes around the remaining two triangles in the opposite direction, which corresponds to two anti-defects. Hence the two configurations can transform into each other.
Here is the video:
In this mode, $\psi$ has five components. A sombrero potential depends on the first two components, another one on the next two. The sombrero potentials are combined additively, with weighting factors depending on the fifth component: At negative values of the fifth component, one potential is more pronounced, and at positive values the other. Another function is added that has minima at $\psi_5 = \pm \sqrt{10}$, so that the fifth component levels out at a modulus of $\sqrt{10}$ with different signs. So again there are domain walls.
The actual formula is: \begin{align} V(\psi)=&\frac 1{1+e^{-\psi_5}} \cdot \left(\psi_1^2+\psi_2^2-1\right)^2 \\ & + \left(1-\frac 1{1+e^{-\psi_5}}\right) \cdot \left(\psi_3^2+\psi_4^2-1\right)^2 \\ &+\frac 12 \left(\frac{\psi_5^2}{10}-1\right)^2 \end{align}
The defects belonging to the first sombrero potential are depicted in white, the ones belonging to the second sombrero potential in black. The size of the defects is determined by the markedness of the associated potential term: The deeper the potential, the smaller the core of the defect. In domains with $\psi_5=-\sqrt{10}$ we thus find large white and small black defects, and vice versa in the other domains.
Because the small defects have more potential energy, energy is released when a small defect passes through a domain wall and becomes a big one. Vice versa, it costs energy for a large defect to change over into the other domain and to become a small one. Hence a traveling domain wall can push a large defect along in front of it. You can see it in the example video at the last domain wall:
Here, too, the last defect pair does not annihilate immediately.
In this mode, the potential is four-dimensional and given as a sum of thee sombrero potentials.
The first sombrero potential depends on $\psi_1$ and $\psi_2$ $\left(\text{as } \left(\psi_1^2+\psi_2^2-1\right)^2\right)$ and has its minima on the cylinder with the equation $\psi_1^2+\psi_2^2=1$.
The second sombrero potential is given by $\left(\psi_3^2+\psi_4^2-1\right)^2$ and has its minima on the cylinder with the equation $\psi_3^2+\psi_4^2=1$, which is rotated isoclinically through $90^\circ$ relative to the first one. The two cylinders intersect in a scaled Clifford torus.
The third sombrero potential is given by $\frac 18\left(\left(\psi_1+\psi_3\right)^2+\left(\psi_2+\psi_4\right)^2-2\right)^2$. It is shallower than the first two and has its minima on a cylinder with the equation $\left(\psi_1+\psi_3\right)^2+\left(\psi_2+\psi_4\right)^2=2$. This cylinder is related to each of the first two by a $45^\circ$ spiral similarity and intersects the Clifford torus in two Hopf circles.
These two circles are the minima of the total potential. Because the set of minima has two separate components, there are domain walls. The two kinds of domains are visualized by greenish and bluish regions, respectively. Point defects corresponding to a loop around the first cylinder are colored red and point defects belonging to the second cylinder are green. Both red and green defects always sit on a domain wall, as going around one cylinder inside the Clifford torus without going around the other cylinder will necessarily lead into regions where the third summand of the potential is not 0, and one will intersect both Hopf circles, so one goes through both domains. This domain wall, however, can contract into a point. Then the red and the green defect will overlap to form a yellow or white point, depending on whether the surrounding domain is greenish or bluish.
For some reason, the yellow or white combined defects interact with domain walls by splitting again into a red ad a green defect which then sit on the domain wall next to each other.
Here is an example video:
This mode only differs from the previous one in the starting configuration.
At the beginning there are two red and two green defects concentrated at a single point, and at a different point the corresponding anti-defects. Each of these quadruple defects is surrounded by a domain wall. As such a double charge is not stable, it splits into two yellow defects, each consisting of a red and a green defect. The two yellow defects repel each other until they hit the domain wall. There they split into a red and a green defect and so get stuck on the domain wall. The domain wall slowly contracts until two opposite sides of the domain annihilate. Only then the red and green defects can join into white ones and repel each other further.
Example video:
(mp4, webm, YouTube)
SO(3) is the set of all matrices that describe rotations of three dimensional space. They are orthonormal matrices, i.e. $M^\top M=\idMatrix_3$. Also the determinant is 1. The potential with the equation $$ V(\psi) = \frob{M^\top M - \idMatrix_3}^2 + (\abs M - 1)^2, $$ where $\frob \cdot$ is the Fronbenius norm and $M$ is a matrix having as entries the nine components of $\psi$, thus has as minima the elements of SO(3).
There are loops in SO(3) that cannot be contracted into a point inside SO(3). These correspond to point defects in the wave equation with that fiber potential. Such a loop is, e.g. a sequence of rotations around any axis, where the rotation angle changes from $0$ to $360^\circ$. Because the SO(3) matrix for a rotation through $360^\circ$ is the same as for a rotation through $0^\circ$, the loop is closed. Realize that such a sequence can not be deformed continuously into a constant sequence, that is the loop cannot be contracted into a point. However, it can be deformed into a sequence that rotates in the other direction, that is form $0^\circ$ to $-360^\circ$. This is easiest seen by imagining SO(3) as a ball where antipodal points of the boundary are identified with each other. A point $P$ in this ball corresponds to a rotation: The direction from the center to $P$ is the axis of rotation and the distance from the center corresponds to the rotation angle, so that the $180^\circ$ rotations are located at the boundary. Then the loop I just described is an oriented diameter of the ball, and you can deform it into a loop of opposite orientation by simply rotating it through $180^\circ$ about an axis of the ball perpendicular to the loop.
The fact that one can simply reverse the orientation of a loop implies that the associated topological defects are their own antiparticles.
So here, different from fiber potential / S¹
, there exists only a single kind of defect, and every defect attracts every other
and can annihilate with every other defect.
Sadly, I did not come up with a good way of visualizing this fact.
The visualization shows the value of the potential in the green channel, the tension energy
in the red channel and the kinetic energy in the blue channel.
Here is an example video:
In this mode the potential is 18 dimensional, corresponding to two 3×3-matrices $N$ and $M$.
The formula is:
\begin{alignat}{3}
V &&= &&& \lambda_m\cdot\left(\frob{M^\top M - \idMatrix_3}^2 + (\abs M - 1)^2 \\
+ \frob{N^\top N - \idMatrix_3}^2 + (\abs N - 1)^2\right) \\
&&&&+ & \lambda_r\cdot\frob{M^\top M - \idMatrix_3}^2\cdot\frob{N^\top N - \idMatrix_3}^2 \\
&&&&+ & \lambda_c\cdot\frob{M^\top N - \idMatrix_3}^2
\end{alignat}
On the first nine dimensions and also on the last nine dimensions, a potential depends like in fiber potential / SO(3)
, weighted with
$\lambda_m=1$. This causes two kinds of defects that are each their own antiparticle.
Added to this is a term that prohibits both matrices to be non-orthonormal simultaneously. This term is weighted with $\lambda_r=10$ and sees to it that the two kinds of defects cannot exist in the same place.
Finally, the term weighted with $\lambda_c=\frac 1{20}$ increases the potential energy whenever the (nearly orthonormal) matrices $M$ and $N$ are unequal. Thus a loop around a single defect has to go necessarily through a region where this term is relatively large. Only if the loop goes around both an $M$ defect and an $N$ defect, every point of the loop may have vanishing potential energy. This causes a band-shaped region of increased energy to exist between two unlike defects. This band strives to be as short as possible. Due to the $\lambda_r$ term, the defects at the ends of the band cannot be at the same place, so they instead form pairs lying close together.
The visualisation renders the defects in red and green, and the potential energy in blue.
Here is an example video:
This confinement
idea can be transferred to defects caused by sombrero potentials.
We will start by considering three kinds of defects with their anti-defects, thus there is a six dimensional potential.
To simplify the description, I combine each pair of components of $\psi$ into a complex number.
Because the cores of the defects later are visualized by red, green, and blue color respectively, I call the complex numbers
$\psi_r$, $\psi_g$, and $\psi_b$ and define them as
\begin{align}
\psi_r &= \psi_1 + i\cdot \psi_2 \\
\psi_g &= \psi_3 + i\cdot \psi_4 \\
\psi_b &= \psi_5 + i\cdot \psi_6.
\end{align}
A sombrero potential can than be written compactly using the definition
$$ m(z)= \left(\abs z^2 - 1 \right)^2.$$
If we want bands of increased energy to exist between individual defects of different kind, pulling them together into groups like above, we have to increase the potential energy whenever the angle inside the minimum circles of the sombrero potentials are unequal. Due to the sombrero potentials, we may assume that everywhere apart from the cores of the defects the complex numbers have a modulus of approximately 1. Hence we may simply use a term of the form $\Re\left(1-\psi_{r}\overline{\psi_{g}}\right)\ \left(\approx 1 - \cos \left(\arg{\psi_r}-\arg{\psi_g}\right)\right)$ in order to cause the $\psi_r$ defects and the $\psi_g$ defects to attract.
The complete potential equation, that causes defects to form groups of three but also to repel on short distances, is as follows: \begin{alignat}{3} V(\psi)&& = &&& \lambda_m\cdot\left( m(\psi_{r})+m(\psi_{g})+m(\psi_{b})) \right) \\ &&&&+ & \lambda_r\cdot\left(\left((m(\psi_{r})+m(\psi_{g})+m(\psi_{b})\right)^2 \\ - \left(m(\psi_{r})^2+m(\psi_{g})^2+m(\psi_{b})^2\right) \right) \\ &&&&+ & \lambda_c\cdot\left( \Re\left(1-\psi_{r}\overline{\psi_{g}}\right) +\Re\left(1-\psi_{g}\overline{\psi_{b}}\right) +\Re\left(1-\psi_{b}\overline{\psi_{r}}\right) \right) \end{alignat} with $\lambda_m=1$, $\lambda_r=3$, and $\lambda_c=\frac 1{10}$.
Here is an example video:
Disclaimer: Real quarks do not work like this at all.
Here, like with the previous mode, there are three colors, but there is a light and a dark version of each.
So the potential is twelve dimensional, and the $\lambda_m$ term is composed of six sombrero potentials.
I shall call the associated complex numbers $\psi_{ru}, \psi_{gu}, \psi_{bu}$ for the light colors ($u$ for up
)
and $\psi_{rd}, \psi_{gd}, \psi_{bd}$ for the dark colors ($d$ for down
).
Only the sum of the two angles of equal color, that is the product of the complex numbers, counts for the confinement. For example, the term for the attraction of red and green defects is $$\Re\left(1-\psi_{ru}\psi_{rd}\overline{\psi_{gu}\psi_{gd}}\right).$$
This causes three defects of different hue to join into a group of three, where the brightness does not matter.
It is however also possible for a defect and an anti-defect of the same hue but with different brightness to join into a
meson
, as on a loop around such a configuration the confinement energy can also vanish.
Here is an example video:
This mode almost works like fiber potential / quarks / confinement
, only that $\lambda$ weighting factors are different and
both $\psi_r$ and $\psi_g$ occur squared instead of simple in the confinement terms. The latter has two consequences:
First, net-like structures of confinement energy form (here visualized in black for a change), in which the point defects are embedded.
Second, the minimal isolated structure, that is the smallest configuration of defects that one can put a loop of vanishing potential energy around, consists
of one red, one green and two blue defects.
The two blue defects repel each other, but are bound by the confinement to the other two defects.
Thus an elongated molecule
forms. Here is a screen shot of a molecule and an anti-molecule from the example video:
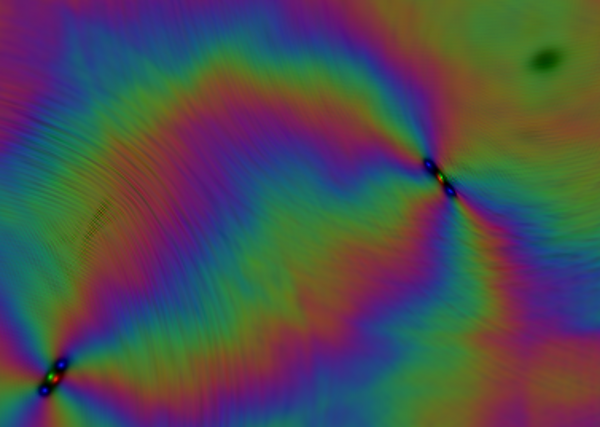
By the way, the dark spot in the upper right corner is a traveling breather soliton, presumably again due to a relatedness to the Sine-Gordon equation. In this case, the relatedness is not so obvious.
The formula for the potential is: \begin{alignat}{3} V(\psi)&& = &&& \lambda_m\cdot\left( m(\psi_{r})+m(\psi_{g})+m(\psi_{b})) \right) \\ &&&&+ & \lambda_r\cdot\left(\left((m(\psi_{r})+m(\psi_{g})+m(\psi_{b})\right)^2 \\ - \left(m(\psi_{r})^2+m(\psi_{g})^2+m(\psi_{b})^2\right) \right) \\ &&&&+ & \lambda_c\cdot\left( \Re\left(1-\psi_{r}^2\overline{\psi_{g}^2}\right) +\Re\left(1-\psi_{g}^2\overline{\psi_{b}}\right) +\Re\left(1-\psi_{b}\overline{\psi_{r}^2}\right) \right) \end{alignat} mit $\lambda_m=1$, $\lambda_r=1$ und $\lambda_c=\frac 16$.
Here is the example video: